I’ve had this blog for awhile, but barely posted in it. I’m tired of this, and it’s strange because the reason I haven’t posted isn’t a lack of things to say, the problem is just plain not getting around to writing anything. So, an experiment: From now on, I’m going to start making a post here every monday. Even if it’s not particularly coherent or long or I don’t have a specific topic and have to just rant out whatever is in my head, that’s fine. If the resulting posts turn out to be terrible, I’ll just stop doing them or bury them in a box deep beneath the earth or something. In the meantime, I’m just going to make an effort to post something here every week from here on out. So if you know me outside of this site, and a monday comes and you realize I didn’t post anything here, find me and yell at me.
Sound good? All right, here goes.
So I’ve been reading all this stuff about physics lately. I haven’t been doing this for any particular reason. At least, not any good reason; the reason I originally started was that I’d been reading a bunch of stuff about evolutionary biology so that I could argue with creationists, but then arguing with creationists started getting kind of boring, so I started looking around for something else to read.
Once I got started, though, it turned out that this is actually a really interesting time to be following physics.
Fundamental physics has been kind of in a holding pattern for about the last thirty years or so. Somewhere in the mid-70s, every single force, particle and effect in physics except gravity was carefully fit together into a single unified theory called the Standard Model, and past that, physicists kind of got stuck. This isn’t to say nothing’s been done in the last thirty years, mind you– experimentally it has really been a productive time– but all the work that has been done has just served to validate the Standard Model, theoretical physics’ last great achievement, as correct. Nobody’s been able to move beyond or supercede the Standard Model. And physicists really, really want to supercede the Standard Model. To even the physicists that developed it, the standard model has always seemed like kind of a Rube Goldberg contraption; it has all these unexplained fiddly bits and extra pieces that don’t seem to do anything, and it’s not clear why any of the parts fit together the way they do. Scientists have a very specific and clear idea of how this big Rube Goldberg machine works; but they don’t know why it works, or rather, they don’t know why the machine is fit together the way it is.
Theoretical physicists are convinced there’s some kind of underlying order to this that we haven’t just figured out yet, and that all the funny complexities of the Standard Model are just emergent side-effects of something much more fundamental and simple going on below the surface. Theoretical physicists are also annoyed that they haven’t been able to figure out how gravity fits in to all to this– in fact, they can’t figure out how to make gravity work together with any theory of quantum physics. So for the last thirty years theoretical physicists have been going to enormous lengths experimenting with grand unified theories and supersymmetric models and such, trying to come up with a better theory that explains the same things the Standard Model explains (and hopefully also gravity), but in a way that makes more sense. None of these attempts have so far worked. They’ve all turned out to not quite be able to predict the actual universe, or else have predicted the universe but with some weird quirk or other that doesn’t exist in reality, things like proton decay.
The longest-standing of these attempts at unification is something called String Theory, which has been worked on steadily for about twenty or thirty years now. String Theory isn’t really a theory– it’s more like a set of hypothetical theories that share certain characteristics. String Theory is really promising in theory and has gotten a lot of attention because it has the ability to describe a universe which has lots of particles and forces (which maybe include the kinds of particles and forces that the Standard Model contains) and which also has gravity, all based on nothing but simple vibrating stringlike objects following simple rules. But there are some problems, foremost among which is that in practice, nobody’s yet figured out how to use this to describe our universe. Every time people try to put together a string theory that might describe the things we see in our universe, it also describes lots of other things, things like lots of extra dimensions that have never been detected and enormous quantities of new kinds of particles that have never been seen. These isn’t exactly a problem because string theories are very flexible and so every time somebody finds a reason String Theory might not work, they can just modify the theory– adding ways of hiding the extra dimensions and particles, and then hiding the weird complexities they used to hide the extra dimensions, such that even though String Theory still predicts most of these things it predicts that they’d be hiding where we couldn’t find them. This has happened enough times by now that String Theory, which started with just some simple rules, has now gotten very complicated. It’s not clear whether this is a good or a bad thing. This might just mean String Theory is maturing, and so naturally picking up complexity as it moves toward completing an actual descriptive and usable theory. Or it might mean we’re on the wrong track entirely with String Theory, and this burgeoning complexity means we’re taking an originally good idea and torturing it into increasingly unrecognizable shapes, adding more and more epicycles every time something doesn’t quite work right, in an attempt to twist the idea into fitting a universe it fundamentally does not describe. Either way, we’re still no more sure whether String Theory can ever actually work than we were two decades ago, String Theory is still more a toolbox of promising mathematical ideas than an actual working theory, and although String Theory gets most of the attention these days it’s still the case that nobody knows how to move past the Standard Model.
Anyway.
This has all been the state of things up until very recently, but right now at this instant early 2007 some kind of interesting new developments are starting to crop up, and it’s starting to look like this holding pattern may be breaking sometime soon. These new developments are making physics very interesting to follow right now, since they mean we might see some new and very dramatic and unexpected developments in physics maybe even in the next year or two.
The first of these developments, and probably the most directly exciting because it involves things blowing up, is the Large Hadron Collider, a 17-mile concrete tunnel buried underneath Switzerland where, starting at the end of this year or beginning of the next, physicists will be smashing hydrogen atoms together to break them apart so they can look at the pieces. Experimental physics has kind of been in a pattern for the last fifty years where most of the progress is done by building a big machine that fires two particle beams at each other, then recording the little tiny explosions that happen when the beams collide and checking to see whether you know enough about physics to explain why those explosions looked the way they did. Once you you’re confident, yes, you can explain the little explosions from your big machine, you build a bigger machine that does the same thing and repeat. The reason this repetitive mode of experimentation has come about is that the most fundamental physical phenomena are only really detectable at very high energies; in a simplified sense, the more “electron-volts” you have, the more interesting things happen. Every time a new particle accelerator is built that can hit a higher electron-volt threshold, new kinds of particles become visible. This is again a bit of a simplification, but particle physics has been in a lot of ways doing this kind of game of particle leapfrog for the last half-century, where the experimentalists will build a bigger particle accelerator and discover some new particles nobody’s seen, and then the theoreticians will have to come up with a theory to explain what those particles are, but then the new theory will predict some new particles nobody’s ever seen and the experimentalists will have to build a bigger accelerator to look for them. There’s a bit of a problem with this system, though, which is that this pattern is strictly dependent on the regular production of these ever-more-expensive accelerators, each of which takes decades to plan and build and hundreds or thousands of people working together to design and operate. This is kind of a lot of eggs to put in one basket, so when the last big particle accelerator that was supposed to have been built– the Superconducting Supercollider, which was supposed to have been built in the 90s– got cancelled amidst massive mismanagement and governmental budget crunches, it kind of screwed the pattern up. (The cancellation of the supercollider has been kind of a factor in why theoretical physics has been in holding pattern mode lately, and also represented a real identity crisis for particle physicists, who for a long time during the Cold War basically had the ability to get as much money as they wanted from the government, while some other branches of science just begged for scraps, because during the Cold War it was considered a national priority that our giant concrete particle beam shafts be bigger and longer than the ones the Russians had.) In the meantime we’ve been stuck with the Tevatron, finished in the mid-80s, which scientists have just continued to use for new experiments. This means we’ve gotten some good chances to explore everything in the energy range up to the Tevatron’s limit of one terra-electron-volt, but nobody’s been able to look past that.
But now the Large Hadron Collider, which can go up to about 15 terra-electron-volts, is going online, with the first operational tests scheduled (link goes to a big pretty graph!) for October of this year. In the short term, this mostly just means probably a bunch of science stories in the news when this all starts up toward the end of the year. But then once a year or few has passed and the real science starts, physics is going to actually start changing. There’s a lot of possibilities of things that could happen– finding supersymmetric partners or tiny black holes or the other exotic things that String Theory and other unification theories predict. Even aside from getting lucky and finding something big like that, though, the big expected purpose of the LHC is going to be to find a particle called the Higgs Boson, which is the only thing in the universe which is predicted by the Standard Model but which has never been actually seen. Finding the Higgs Boson would be a big deal, among other things because part of what the Higgs does is cause things to have mass, so once we’ve found one and nailed down its properties this might be a push in the right direction for the people trying to figure out how to make the standard model play nice with gravity. The other, unbelievably frustrating but actually probably even more promising possibility is that the LHC won’t find the Higgs Boson. This would be a big deal because it’s starting to look like if the Higgs Boson can’t be found at 15 terra-electron-volts, then it very probably doesn’t even exist, meaning theoretical physicists would have to go back to the drawing board in a potentially big way.
Aside from all this, a second interesting ongoing development in physics is that, while all these problems with accelerators have been going on, a whole bunch of rich and occasionally just plain crazy experimental results (and pretty pictures) have been showing up in astronomy thanks to advances in space-based telescopes. Astronomers have been undergoing a quiet renaissance in the last ten years after the Hubble Space Telescope finally started working, turning up all kinds of stuff that– although physicists haven’t really managed to find any clues forward in it yet– provide some big juicy questions that the next breakthrough in physics might be able to make a go at tackling. The biggest of these is the discovery of “dark energy”, the idea behind which can be summarized as “the universe’s expansion is speeding up over time, and we have no idea why“. It’s not clear whether this recent period of rapid advancement in astronomy will be able to continue much longer, since between the upcoming scuttling of Hubble and the gradual shifting of science research out of NASA’s budget it’s now questionable whether some of even the really promising experiments planned to follow up on the Hubble discoveries will be able to actually get carried out. But even still, we should expect at least a couple upcoming surprises from those experiments that do manage to get launched.
A third, less concrete and more sociological development in physics lately has been the new backlash against String Theory, typified by (or maybe just consisting of) two new and “controversial” books by Lee Smolin and Peter Woit. String Theory has always had detractors, but lately– partially in response to some documentaries in the late 90s where String Theory physicists took their ideas to the public, partially as a result of the increasingly long period of time String Theory has gone now without predicting anything concrete, and partially in reaction to the recent embrace by many string theorists of a really, really bad idea called the “landscape”– a handful of these detractors have started making their case against String Theory in a very public and organized way, and a lot of average members of the public (like, well, me) are starting to take notice. So far this String Theory Counterrevolution doesn’t really seem to have had any real effect on the state of science itself; its chief byproduct seems to have been a series of blog wars between physicists. (Though, if the reason I’m mentioning all of this is to list some of the things that have made physics interesting to follow lately, it’s definitely the case that watching PH.Ds with decades of experience flame each other on their blogs is entertaining, in a pro-wrestling sort of way.) Still, the way this backlash against string theory has played out does seem to hint we may indirectly see some interesting advancements in the near future; many or all of the people speaking out against string theory lately have been doing so under the auspices of arguing actually not that String Theory is outright wrong or should be dropped, but simply with the intent of trying to argue that additional approaches to fundamental physics should be explored as well– many of the string theory backlashers are themselves incidentally proponents of still-embryonic alternate approaches, usually Loop Quantum Gravity in specific. Considering that these arguments are being made in the full hearing of the public and other people who are responsible for the actual funding of physics, there may soon be a bit more oxygen for these alternate approaches for to get the attention and funding needed for serious progress, so we may see some interesting developments coming from them before long.
The last kinda-interesting development in physics of late is the one that actually inspired this blog post and long tangent, which is the emergence of quantum computing as an active research field which may sometime soon actually produce useful machines. Basically, while particle physicists have been busting their asses trying to convince the government to buy bigger magnets and theoretical physicists have been gothing it out about their problems with strings, a lot of applied physicists, people in areas like quantum optics, have just been quietly doing their jobs and, although maybe not working on as large a scale as some of those other groups of physicists, actually getting shit done. One of these busy areas has been quantum computers, which over the last few years has undergone some really dramatic advances, from the first working programs running on a quantum computer in only 1998, to two years later it being a big deal when quantum computers with five or seven qubits were able to factor numbers up to 15, to by this year people getting all the way up to realistic levels like 16 qubits and sudden advances happening in things like memory transfer or gates for quantum computers. This is all a really intense rate of progress– it was not long ago at all that quantum computers only existed as buzzwordy black boxes used by science fiction authors, who assigned them improbable capabilities– and there’s not really any telling what exactly happens next.
Quantum computers work by storing information in the quantum states of various physical things. This is useful because of the weird ways quantum states act. Information in a traditional computer is stored using physical things themselves, like holes in a punchcard, or tiny pits on a DVD surface, or electricity in a capacitor in a RAM chip. Each of these different ways of physically encoding data, when you store a “bit” of information, it’s either a 0, or it’s a 1. Either there’s a pit in the DVD surface, or there’s not. Quantum states, on the other hand, are not necessarily one single thing at a time; when you store data as a quantum state, what you instead store is a probability that that quantum bit (qubit) is 0 or 1. This means that when you store a number in a qubit register, you don’t have to store just one number in there; you can store lots of different numbers, as superpositions of probabilities. This leads to lots of crazy possibilities, since it means a program running on a quantum computer can, in a sense, do more than one thing at the same time. In another sense, this is just fakery; you’re not actually doing more than one thing at once, you’re just probabilistically choosing one of a certain number of possible paths the program could have taken. This leads to another weird property, that quantum computers don’t always return the right answer– they at best just have a certain known probability of returning the right answer. But probabilistic algorithms actually are a real thing in computer science, and can be fundamentally faster than traditional ones, so this is actually okay: you can run a quantum algorithm over and over and average the result, and you’ll still get the right answer way faster than you would have with a traditional computer.
The thing is though that working with quantum states as quantum computers do is actually really, really hard. Quantum superposition is usually described to people using a thought experiment with a cat in a box and lots of big macroscopic objects like geiger counters and vials of poison, but this is mostly just a metaphor and it’s never anywhere near that easy to set up. There’s this “observation” in the Schrödinger’s cat thought experiment that collapses the waveform and forces the cat to be either alive or dead; this is usually described as “opening the box”, but actually any interaction whatsoever between the systems inside and outside the box, including stray heat propagation or vibrations in the air (say, from the cat yelling to be let out of the box) while the box is still closed, is enough to entangle the systems and collapse the waveform. Theoretical physicists doing thought experiments may get to gloss over these little details, but when doing quantum computing, these little details become incredibly practical and immediately relevant– because they mean that if the qubits in a quantum computer interact with their environment, ever, in any way, then the quantum state is destroyed and your computation is erased. This means that whatever things hold the qubits in your computer have to be effectively totally isolated from quantum interference of any kind, and continue to be so while doing gobs of things that normally no one would want, need, or try to do with a quantum state, like transport or copy it. Figuring out how to do this, and all the other things that quantum computing entails, means really stretching the edges of what we think we know about quantum physics, and means that quantum computing has actually become something of a hotspot for theoretical physics researchers at the same time that “normal” theoretical physics has been struggling to progress. I’m only able to perceive all of this from a far distance, of course, but still it’s been interesting to watch.
It’s been particularly interesting to me, though, because at the same time theoretical physics is getting a workout in the applied problem of building quantum computers, something else is getting a workout in the related applied problem of what to do with the quantum computers after they’re built: theoretical computer science. Theoretical computer science and computability theory is something I actually personally know something about (unlike, it is worth noting, quantum physics), and it’s incidentally a topic which gets very little attention. Computer science professors often do their best to convince the students passing through that things like turing machines and lambda calculus actually matter, but people don’t get computer science degrees to do computer science theory, they get computer science degrees to get a job programming– and in a day to day practical sense, aside from an occasional vague awareness of the existence of “big O” notation, the vast bulk of people doing programming have little use for or awareness of computation theory. There are specific domains where this stuff is still directly useful, and there were times in the past where this stuff was still directly practical and relevant, but on average, outside of pure academia, the underlying theoretical basis of computer science these days practically seems to mostly only exist for the construction of intellectual toys for geeks like me who apparently don’t have anything else to do. Quantum computing, however, means that all this foundational computer science stuff not only has become suddenly very relevant and useful, but also suddenly has a bunch of new and relatively accessible open questions: As far as I’m aware no quantum algorithms even existed before 1993, and there’s still a lot of important questions to be answered on the subject of, once quantum computers “work”, what the exact extent of their capabilities might be and what we should do with them.
So to me personally, quantum computing is kind of interesting on two levels. One, if I’m going to treat the science of physics as a spectator sport, then from a spectator’s perspective quantum computers are one of the more interesting places things are going on right now; two, because of the connection to pure computer science, I or other people familiar with computers or programming actually have a chance of directly understanding what’s happening in quantum computers, whereas with, say, the Higgs Boson (which really? I’ve seen no fewer than five distinct attempted explanations of the Higgs Boson now, and I still have no clue what the darned thing really is), we’re left mostly only able to read and repeat the vague summaries and metaphors of the people who’ve worked with the underlying math. And then there’s a third thing I can’t help but wondering about in the interaction between these two things: I’m wondering if someone like me who already understands computers but doesn’t understand physics might be able to use quantum computing as a way of learning something about quantum physics. Real quantum physics takes years of really hard work and really hard math to learn, and most colleges don’t even let you at this math until you’ve already dropped a significant amount of time investment into the low-level, more accessible physics courses; on the other hand, if you’re outside of a college and trying to learn this stuff on your own, it’s very hard to find sources that really tell you directly what’s going on instead of coddling you in layer after layer of increasingly elaborate metaphors. Metaphors of course are and should be a vital tool in learning physics, but when you come right down to it physics is math, and glancing at most materials on quantum physics, I tend to get the feeling I’m learning not quantum physics, but just learning an elaborate system of metaphors, which interact with all the other metaphors as archetypical symbols but are connected to nothing else. On the other hand, stuff on quantum computing has to actually work with the real-world nuts and bolts and math of quantum physics (unlike popular books on the subject), but because so much of it has to be worked with by computer scientists, non-physicists, at least some of it is surely going to be necessarily aimed at a lower level of background knowledge (unlike learning this stuff at a college would be). One would have to be careful not to fool oneself into thinking this could actually be a substitute for a full physics education, of course, but from the perspective of an interested spectator I can’t help but wonder if this might be a good way of sneaking into the world of higher-level physics through the back door.
This is all a roundabout way of leading up to saying that I’ve been looking into some stuff on quantum computing, and I’m going to try to use what little I’ve worked out so far to try to make a little toy model computer simulation thing, which I will then post about it here, on the internet, along with some hopefully psychedelic animated GIFs the simulation generated. If I’ve kind of got things right, then putting this post together in a form other people can hopefully understand will help me get my thoughts in order and test what I’ve got so far (I’m allowing myself the presumption of assuming anybody’s still reading at this point); if I’m just totally confused and wrong, meanwhile, then hopefully somebody who understands this stuff will eventually find this and point my mistakes out. A first little attempt at this is below.
Specifically, I’m curious whether one could define a quantum version of Conway’s Game of Life.
Conway’s Game of Life
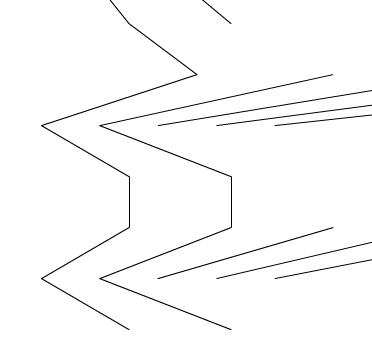
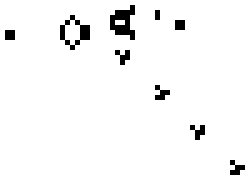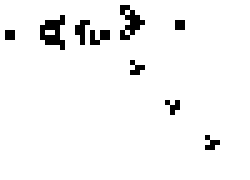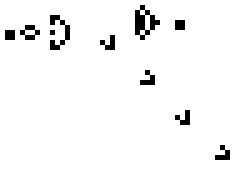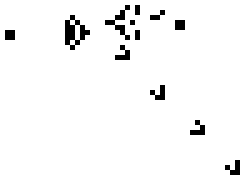 “Life” is this thing this guy named John Conway came up with in the 70s. It’s referred to as a “game” because originally that’s more or less what it was; Conway originally published it as a brainteaser in Scientific American, intended to be played by hand on graph paper, with the original challenge being a $50 reward to the first person who could devise a Life pattern that continued growing endlessly no matter how long the game went on. Conway at first expected this was impossible; he was horribly, incredibly wrong. (An example of such a pattern is at right.)
“Life” is this thing this guy named John Conway came up with in the 70s. It’s referred to as a “game” because originally that’s more or less what it was; Conway originally published it as a brainteaser in Scientific American, intended to be played by hand on graph paper, with the original challenge being a $50 reward to the first person who could devise a Life pattern that continued growing endlessly no matter how long the game went on. Conway at first expected this was impossible; he was horribly, incredibly wrong. (An example of such a pattern is at right.)
Despite these fairly simple origins, Life turned out to be sort of the tip on the iceberg of an entire category of mathematical systems called “cellular automata”, which are now a recognized tool in computation theory and which have received by now a fair amount of attention; Stephen Wolfram, the guy who created Mathematica, spent ten years writing a very long book all about cellular automata (a book which, although I’ve seen a lot of doubt as to whether anything in the book is actually useful to any domain except computation theory, is universally agreed to contain lots of pretty pictures). Life itself has remained the most famous of these; today there are entire websites devoted to categorizing Life patterns of every kind you could think of, and most people with an education in programming have been forced to implement a Game of Life program at one point or other.
- - - - - 1 2 3 2 1
- O O O - 2 3 4 2 1
- O - - - -> 2 4 5 3 1
- - O - - 1 2 2 1 0
- - - - - 0 1 1 1 0 |
| On the left is a grid of cells containing a glider; on the right is a grid containing the count of living neighbors that each cell on the left has. I’ve colored light red the dead spaces which in the next generation will be new births, dark red the live spaces which in the next generation will survive, and light blue the live spaces which in the next generation will die. Let this keep running a few more generations and you get the glider: |
The term “cellular automata” just refers to systems that can be described by patterns of colored dots in “cells” (i.e., grid squares or some other shape on graph paper) and which change over “time” (i.e., redrawing the system over and over on pages of graph paper) according to some simple rule– in all variations of cellular automata I’ve ever seen, how a cell is colored in one frame depends on how its neighbors were colored in the previous frame. In the original Conway’s Life, the rule was that a cell is colored black in a new frame if
- in the previous frame it was colored black and was touching either three or four cells colored black, or
- the cell was colored white in the previous frame but was touching exactly three cells colored black.
Conway intended this as a sort of population model (of “life”) where black dots represented living things; black dots disappearing when they have too few or too many neighbors represent that lifeform dying of either loneliness or starvation, black dots appearing when they have a certain number of neighbors represent reproduction.
 |
These rules favor non-life over life, so if you just fill a board up with randomly placed live and dead squares, within a couple of generations most of the life will have died off or settled into tiny static patterns, like little solid blocks or little spinners eternally looping through a two-frame animation. But you’ll also have little areas that wind up filled with sloshing waves of chaos, breaking against and devouring the static bits. If you watch this carefully, you’ll notice that chaotic as these waves look, the way Life patterns act when they collide with one another is actually very specific and structured. The systems in Life are chaotic enough that predicting what a random Life pattern you come across is going to do is just about always going to be impossible unless you sit down and actually run it. But if you sit down ahead of time and work out a catalog of patterns that you know what they do and how they interact with other patterns, and then stick to placing those patterns in very carefully controlled ways and places, you can actually use these smaller parts to design larger life patterns that have basically whatever behaviors you want.
 |
You can build machines.
Life is an example of something we call a “model of computation”, which is a name we give to systems– machines, language systems, board games, whatever– that can be one way or another tricked into running some kind of “program” that’s dummied up for it, such that after a while its changes in state have effectively computed some sort of result. The kinds of computational models we normally care about are the ones that we say are “Turing complete”. This is a reference to the first ever proven universal model of computation, the Turing Machine devised by Alan Turing in 1936. The Turing Machine is a hypothetical computer, described as a sort of little stamping machine on wheels that slides back and forth on an infinite tape reading and rewriting symbols according to a little set of rules it’s been wired up with. The Turing Machine was not meant to ever actually be built; it was designed just to be easy to reason about and demonstrate interesting things in mathematical proofs. The most interesting thing about the Turing Machine is that it is in fact universal; there’s a generally accepted but technically unproven principle called the Church-Turing Thesis that any programming language, computer, whatever, that you can think of, can be emulated on a Turing Machine. This makes the Turing Machine suddenly really important as a sort of least common denominator of computers, since if you have a machine that can emulate a Turing Machine– in other words, a machine which is Turing complete– then that machine can inevitably emulate anything a Turing Machine can, including every other Turing complete machine, as well. Turing Complete models of computation are as common as dirt– they include every computer and programming language you can think of, as well as some really bizarre and deceptively useless-looking mathematical systems, a couple of which Conway invented— and they’re all approximately the same, because they can all do exactly those things the other Turing complete systems can.
The Game of Life is, as it happens, Turing complete, as was quite dramatically demonstrated a few years back when some guy actually built a Turing Machine that runs inside of a Life system. The Life Turing Machine is a machine in a hopelessly literal sense; viewed zoomed out, it looks like some kind of aerial photograph of some steam-powered contraption that a man from the 1800s with a handlebar moustache would demonstrate, after dramatically pulling off the canvas that covered it. The thing isn’t particularly efficient; if you for some reason took the time to make an emulator for an 386 Intel PC out of Turing machine rules, and then ran this emulator on the Life turing machine, I imagine the heat death of the universe would probably come before you managed to get Minesweeper loaded. But efficiency isn’t the important thing here: it works, and that’s what matters.
Something worth noting is that, although I’ve already claimed that turing machines are approximately the same as any computer you can think of, this isn’t quite true– quantum computers actually aren’t included in this generalization. Normal computers can emulate quantum computers, but only with unacceptable amounts of slowdown (insofar as certain kinds of proofs are concerned), and there are things quantum computers can do but normal Turing-complete machines outright can’t, specifically generate truly random numbers. This isn’t a problem for the Church-Turing thesis, exactly: We can just get around this by saying that the Church-Turing thesis is only supposed to describe deterministic machines, which quantum computers aren’t. Despite this, we still have to have some kind of least common denominator to reason about quantum computers with, so we have this thing called a Quantum Turing Machine that vaguely resembles a Turing Machine but is able to provide a universal model of computation for quantum computers.
So, all this in mind, here’s what I wonder: The Turing Machine is a universal model of conventional computation, and you can make minor modifications to the turing machine and get something that’s also a universal model of quantum computation. Life is also a universal model of conventional computation; you can make a turing machine in it. Is there some simple bunch of modifications that can made to Life that make it a universal model of quantum computation?
I originally started wondering about this in the context of Loop Quantum Gravity, something I mentioned earlier as an “alternative”, non-String theory of Physics. Loop Quantum Gravity is supposed to be a theory of Gravity that incidentally follows the rules of Quantum Physics. This is something that is understood to be either extremely difficult or impossible, for a couple reasons, one of which is that gravity has to play nice with the Theory of Relativity. The Theory of Relativity plays hell with quantum theories because it says the geometry of the universe is bending and warping all the time like silly putty, which makes the quantum theories scream “I CAN’T WORK UNDER THESE CONDITIONS!” and storm out of the building. Loop Quantum Gravity, at least as I understand it, gets around this in part by quantizing geometry itself– that is, it makes the very geometry the universe exists inside subject itself to a form of quantum behavior. One of the consequences of this as I understand it is that the geometry of the universe becomes discrete, which kind of means that it can be represented as if it were a big interlocking bunch of (albeit really weirdly shaped) cells on graph paper. In other words, you could if you really wanted to treat the geometry described by Loop Quantum Gravity as a board to run Life on. If true, this seems like an interesting idea to me because Loop Quantum Gravity is really hard to find any remotely accessible information on and all the information that is available is super high level math, so it seems like something like Life or some other cellular automata running on the nodes of a LQG spin network would be a fun little visual demonstration of how the thing is supposed to work. But before you did that, I assume, you’d have to have some kind of conception of what a cellular automata in a quantum universe would work like at all.
A Quantum Game of Life
Conveniently, creating cellular automata with quantum behavior isn’t at all a unique idea; looking around I’ve found that people have been working with QCA models almost as long as they’ve been working on Quantum computers, and several conceptions of cellular automata with quantum behavior are already around. I’m going to list them here, since I used some of them in formulating what comes after.
- First, there’s the universal quantum turing machine itself. Mark Chu-Carroll has an informal but very clear explanation here of how the quantum turing machine conceptually works; you can also find the original paper that first defined the QTM online under the title Quantum theory, the Church-Turing principle and the universal quantum computer. It’s a bit of a heavier read, but the introductory parts are plain readable everyday English and interesting for their own reasons.
- On top of this, there’s actually real ongoing research into what are called “quantum cellular automata” or “quantum dot cellular automata”. If you’ll look into these, you’ll find they seem to mostly consist of systems of little objects that look like dice arranged next to each other like dominoes, such that the painted dots in any individual die change color over time depending on how the dots in the closest adjacent die are colored. I’m not exactly sure how these things work, but I do notice two things. One, this version of cellular automata looks very serious and formal and appears to have real practical application in actually simulating quantum systems. Whereas what I’m hoping to make here is more a silly little toy program that makes pretty pictures. Two, doing anything in this version of QCAs seems highly dependent on how you arrange the tiling of the dominoes against each other, whereas I’m really hoping for something where the behavior is dictated by the way the “lifeforms” are positioned and not by the way the external geometry is preconfigured.
- Some guy named Wim van Dam in 1996 actually wrote an entire Master’s thesis on the subject of quantum cellular automata, under the simple title of “Quantum Cellular Automata“. Van Dam’s thesis there is actually well worth reading if you’re finding any of this so far interesting, and explains the motivations and workings of quantum computers, cellular automata, and hypothetical quantum cellular automata all way better than I do here– probably to be expected, since it’s an entire master’s thesis, instead of just a “this is how I wasted my Saturday” blog post. Potentially extremely conveniently for my purposes, Van Dam actually describes specifically how to formulate a one-dimensional cellular automata of the exact kind that the Game of Life uses. He does not, however, bother generalizing this to two dimensions as would allow one to implement the game of life in specific, since of course the one-dimensional version is sufficient for his goal of proving the QCAs work.
- Google incidentally turns up a short and concise 2002 paper titled “A semi-quantum version of the Game of Life“. Looking over this, however, it doesn’t appear to be exactly the thing I’m looking for (i.e. a reformulation of Life with quantum style rules). Instead, the paper suggests that such a thing is probably not a good idea, noting “A full quantum Life would be problematic given the known difficulties of quantum cellular automata” (uh oh), and instead takes the opposite tack, of trying to design a quantum system that can simulate life: specifically, they design a way of creating systems of quantum oscillators which interfere with one another in a way which “in the classical limit” exactly follows the rules of life, but which otherwise exhibits various interesting quantum mechanical properties as a result of the oscillators it’s made out of. Which is all interesting, but it isn’t quite what I was looking for (at least I don’t think so), and it also requires one to understand the quantum harmonic oscillator (which I don’t).
None of this exactly provides what I was looking for, since all of the attempts above, as it happens, are by people doing actual physics research. They’re thus doing their work under the constraints of a set of fairly serious goals, goals like applicability in proving things about quantum physics or even implementability as a real-world device. When I think about deriving a version of quantum Life, though, I’m just thinking of something that would be easy for me to implement and useful and fun for demonstrating things. This means that if I’m going to try to construct my own version of quantum Life, I’m going to be working off a somewhat more modest set of goals:
- Just as in the original game of Life, whatever the basic rules are, they should be simple to understand and implement even to someone who doesn’t necessarily understand quantum physics and turing machines and such.
- Also like the original game of life, running a simulation of quantum life should produce pretty pictures.
- And also like the original game of life, the way patterns evolve should exhibit some sort of structure which could be potentially used by someone with lots of time on their hands to design starting patterns with arbitrary complex behaviors.
- The game should incorporate or exhibit some kind of behavior of quantum mechanical systems. Hopefully the quantum behavior should incidentally impose some kind of interesting limitations or provide some kind of interesting capabilities to someone trying to design starting patterns that wouldn’t be the case in standard Life. In the best of all possible worlds it would be possible to demonstrate some interesting feature[s] of quantum mechanics by setting up quantum Life patterns and letting them run.
- Ideally, hopefully, this simple quantum life should turn out to be a model of quantum computation– that is, it should be possible to simulate a quantum turing machine and thus emulate any quantum computer using this quantum life. Since (the Wim Van Dam paper proves this) it is possible to simulate a quantum turing machine on a universal quantum cellular automata and vice versa, it should be sufficient to show any of the “real” QCAs described above can be implemented or simulated as patterns in quantum life.
My first attempt at this follows; to test it, I did a quick and dirty implementation in Perl. Note that although I’m pretty confident of everything I’ve written in this blog post up to this point, after this point I’m in uncharted territory and for all I know everything after this paragraph is riddled with errors and based in gross misunderstandings of quantum physics. In fact, since as I type these words I haven’t actually started writing any of the Perl yet, I have no idea if this quantum Life thing is even going to work. (Though even if it doesn’t, I’m posting this damn thing anyway.)
(Update, Feb 2009: So, I wrote this post a couple years ago when I was first trying to learn about quantum physics and quantum computing, and I actually did make a couple mistakes. The one really huge mistake I made occurs a few paragraphs back, and it propagates forward into the part of the post that follows. The mistake is this: I claim in this post that a qubit in a quantum computer can be described by the probability that that bit is 0 or 1. This is close, but not right. A better way to put this is that a qubit can be described by a quantum probability that the bit is 0 or 1. What is the difference? Well, a normal probability is just a number between 0 and 1– like, 30%. However a quantum probability is a complex number– a number with an imaginary part– of absolute value less than one. This unusual notion of a “probability” turns out not only to make a big difference in the behavior of quantum systems, it’s the entire thing that makes quantum computers potentially more powerful than normal computers in the first place! Unfortunately I didn’t clearly realize all this when I wrote this blog post. So in the final part of this post, I try to define a “quantum” cellular automata– but since at the time I misunderstood what “quantum” meant, I wind up instead defining a cellular automata model which is in fact only probabilistic. Now, given, I think what follows is still kinda interesting, since the probabilistic cellular automata turns out to be kind of interesting unto itself. And it’s definitely a first step toward quantum cellular automata. But, just a warning, it’s not itself quantum. I did later took some first steps toward implementing an actual quantum cellular automata, but they’re not done yet. So hopefully someday I can revisit this and write another post in this series that gets it right this time.
If you want a clearer explanation of this whole “quantum probabilities” thing, I suggest you read this, which is about the clearest explanation of what the word “quantum” means I’ve ever found.)
The most logical way to construct quantum life, at least as far as I’m concerned, is to just take the trick used to create the QTM and apply it to the Life grid. In a Post machine [2-state Turing machine], each tape cell is equal to either state “0” or state “1”; in the QTM, the tape cell is essentially equal to a probability, the probability that the tape cell contains state “1”. This simple conceptual change, from states to probabilities of states, provides basically all of the QTM’s functionality. In Life, meanwhile, as in the Post machine, each grid cell is equal to either state “0” or state “1”; a naive quantum Life, then, could be created by just setting each grid cell essentially equal to a probability, the probability that the grid cell contains state “1” (“alive”). This is the tack I’m going to follow. I’m going to speak of cells below as being “equal” to a number between 0 and 1; when I do this, the given number is the probability, at some exact moment in time, that the cell in question is “alive”.
The introduction of probabilities like this even just by itself offers a lot of opportunity for the creation of new and elaborate cellular automata rules, say rules where each varying number of neighbors offers a different probability of survival into the next generation; I imagine the people who’ve already done so much elaborate stuff with just the addition of just new discrete colors to Life could have a field day with that.
I’m going to ignore those possibilities, though, and just maintain the rules from “Real Life” entirely unchanged– that is, a cell is created iff it has three neighbors, a cell survives iff it has three or four neighbors. These rules still work perfectly well even though now some cells are only “probably” there, and conveniently, this selection of rules means that this kind of quantum Life is in fact completely identical to normal life, so long as all the cells are equal to exactly 0 or exactly 1. The simulation only behaves differently if at least one cell, from the beginning, is programmed to be “indeterminate”– that is, to have some probability of being alive between 0 and 1. When this happens, then we can no longer calculate an exact number of neighbors for the cells in the vicinity of the indeterminate cell. We deal with this situation simply: instead of calculating the number of neighbors, we calculate the probability that the number of neighbors is “right” for purposes of the cell being alive in the next generation. That probability then becomes the cell’s “value” in the next generation. For example, let’s say an empty cell has two neighbors equal to 1, and one neighbor equal to 0.5. This empty cell has a 50% probability of having 2 neighbors, and a 50% probability of having 3 neighbors. Since the cell needs exactly three neighbors to reproduce, the probability of the cell being alive in the next generation will be 0.5.
The questions that immediately come to mind about this way of doing things are:
- Does the addition of “indeterminate” states actually have any interesting or useful effect?
- Is the addition of these indeterminate states to Life sufficient to allow the emulation of a QTM or UQCA?
- Does this actually have anything to do with quantum physics?
- Is this different in practice from the “semi-quantum life” linked above?
- Though one of my goals is for the rules to be simple, and they seem simple to me, I took three long paragraphs to describe these rules. Is the way I described the rules at all clear, and maybe is there some way I could have just summarized them in a couple of sentences?
(As far as the second question here goes, it occurs to me that what I’ve designed here may well not really qualify as “quantum life”, and maybe “probabilistic life” would be a better way of describing it. In fact, looking on Google for the phrase “probabilistic game of life”, I now find that a couple of people who’ve attempted rules along these lines: There’s this little writeup on a math site here, which appears to be describing a version of probabilistic Life with my exact rules. This author doesn’t provide an implementation, though, so I shall press on, although that site does provide some interesting proofs about the behavior of a probabilistic life that I’m not going to bother trying to understand just now. On an unrelated note, Google also turned up this odd little thing, though what it actually specifically has to do with the Game of Life is not obvious from the link.)
Anyway, let’s look at an actual implementation of this kind of quantum life and see the answers to my questions here are at all obvious.
I happened to have this simple implementation of Life sitting around I’d made awhile back, as a perl module that takes in grids containing Life starting states and spits out animated GIFs. This particular implementation was written such that on each frame, the module would make a table listing the number of neighbors each cell in the grid has, then use this number-of-neighbors table to generate the alive and dead states in the next frame. Modifying this existing module to work with quantum life turned out to be incredibly simple: Rather than the number-of-neighbors table being a simple number, I just switched it to being a probability distribution, an array of ten values representing the probabilities that that cell had zero through nine neighbors respectively. I build up this array by starting out with a distribution giving 100% probability of zero neighbors and 0% probability of any other number, and then factoring in the changes to the probability distribution caused by each of the cell’s nine neighbors, one at a time:
0 neighbors:
1 neighbor:
2 neighbors:
3 neighbors:
4 neighbors: |
= |
1
0
0
0
0 |
+
100%
alive
neighbor |
0
1
0
0
0 |
+
100%
alive
neighbor |
0
0
1
0
0 |
+
50%
alive
neighbor |
0
0
0.5
0.5
0 |
+
50%
alive
neighbor |
0
0
0.25
0.5
0.25 |
(If you squint real hard, you can probably see the binomial distribution in there.)
The probability of the cell being alive in the next generation is then calculated by
(probability of cell having 3 neighbors this generation) + (probability of cell being alive this generation)*(probability of cell having 4 neighbors this generation)
What happens when we run this?
Well, at first glance at least it doesn’t appear to work all that well. Here’s what happened when I took a simple glider and placed it on a quantum Life board, in each case varying the probability that the glider was “there” (and, in the last couple cases, varying the probability that each of the “empty” cells were actually filled). In this table I show first the starting condition, and then an animated GIF showing what happened when the Life simulation ran. In each frame, the darker the pixel, the more probable it is that there was a living cell there at that exact moment.
| 100% |
50% |
75% |
90% |
100% |
0.001% |
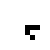 |
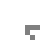 |
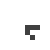 |
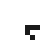 |
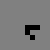 |
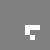 |
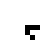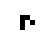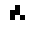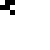 |
 |
 |
 |
 |
 |
The 100% alive glider, as expected, behaves just as it would in normal life. The other gliders… well… just kind of instantly explode. The 90% glider manages to actually on average complete a couple of halting steps before it falls apart entirely, the poor thing, but it too smears out of apparent existence within a few more frames. This in retrospect isn’t actually surprising. When the gliders “disappear”, they’re not outright gone; instead, the blank area where they once were (and a gradually spreading portion of the rest of the blank area, as well) is equal to a bunch of incredibly low probabilities, so low they’re indistinguishable from pure white. This happens because when we run a game of Life containing indeterminate states, we’re basically simulating every single possible board configuration that could have existed at once, with some just being more likely than others. The Life rules favor non-life over life, so the vast majority of these possible games wind up just rapidly spinning out into nothingness– or, at least, the possible games that wind up containing some living cells left don’t have the life settling in some areas any more prominently than others, so the blankness is able to dominate essentially without opposition.
So this version of Life doesn’t at first glance seem to turn out to be very useful in terms of creating a usable or playable game. We could maybe fix the “everything dies instantly” problem by fiddling with the rules some in the next version, though, so maybe things aren’t hopeless. In the meantime, does what we have so far at least demonstrate quantum behavior? Well, it does seem pretty clear that the life cells participate in self-interference, at least from informal observation:
| Starting state |
Center line is 100% there |
Center line is 99.99% there |
 |
 |
 |
At least self-interference is the way I interpret the sort of gradienty behavior the version on the right engages in before it fades out entirely. The probabilities don’t do that whole square-of-complex-numbers thing, and there isn’t anything resembling observation or wavefunction collapse (I could change the GIF-making function such as to basically assume the wavefunction collapse happens on every frame, by randomly populating the gray areas with life instead of displaying the probability distributions, but that would probably just make things visually confusing without conveying anything interesting), but (although I could be wrong about this) the quantum turing machine doesn’t as far as I can gather really have any of these properties either so we could maybe just shrug that off.
Even so, there really doesn’t seem to be any way you could make a turing machine out of parts that keep fading out of existence, so after encountering this everything-fades-away problem I was just about to give up and declare the whole thing a wash. Still, turing machines aside, I did manage to at least find one interesting thing about this particular quantum life implementation. We see the first glimpse of this when we try populating a Life board at random:
 |
 |
Okay, now here there seems to be something going on. You’ll notice that most of these areas actually don’t fade right to white, but instead stabilize at what looks like a sort of 50% gray (although, while they look like it, the stable half-gray spots aren’t 50/50 gray– each of those cells are about 34.7583176922672% there. I don’t know why it’s that particular number, but I assume it has something to do with the tension between the “survivable” thresholds of three and four neighbors.) of probability; apparently there’s some kind of sweet spot there where life boards filled to a certain density of living cells tend to keep that density more or less consistently on average. A few little bits of area stabilize toward zero, though, and the areas of zero gradually eat away at the areas of half-life until there’s nothing left. So that’s kind of interesting. But the one thing that suddenly and out of nowhere justified this entire silly little project to me is what happened when I randomly populated a board, and then “rounded” most of it– that is, I rounded everything on the randomly generated board to exactly 1 or 0, except for a thin little strip of indeterminacy running vertically down the right side. And I got this:
 |
 |
…WTF?
What happens here is that the “probably there” areas converge on the mysterious 34.7% half-life value and then just kind of spill outward, swallowing up all the actually-living cells as they go. Then, once all the living matter has been devoured and no food is left, the white starts eating in and the areas of half-life slowly die out. In other words…
Holy crap! It’s a zombie apocalypse simulator!
So, I’m not sure this entire exercise was altogether productive in any way, though I’m going to keep experimenting with all of this– maybe trying some alternate Life rules besides just Conway’s 23/3– to see if I can coax anything useful out of this quantum Life concept. Check again next week to see if I come up with anything. In the meantime, though, at least, I think that the final image makes the whole thing satisfying to me in two ways:
- I at least got my psychedelic animated GIFs
- I tried to test quantum physics, and instead accidentally created zombies. Does that mean I qualify as a mad scientist now?
If you want to run any of this stuff yourself, you can find the messy little quantum life module here and the script that generated all the images on this page here. You’ll need to rename those files to qli.pm and gliders.pl, and you’ll need Perl and GD::Image::AnimatedGif to run them; and to do your own tests you’ll have to modify gliders.pl. If you need any help with that, just ask below.