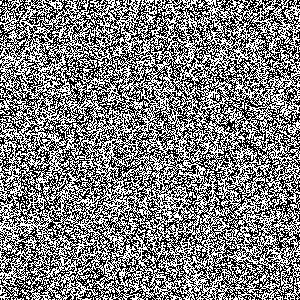So last week I made a little custom variation on an old computer program called the “Game of Life”, with the hopes that my version could be used to demonstrate neat things about quantum physics. As chronicled in my last blog post, that basically didn’t work at all. However, despite not working the way I’d hoped it did, the program did incidentally happen to burp out some very pretty looking animations. This week I figured I’d just say screw the quantum physics stuff, and instead just explore what kinds of interesting pictures I could tease out of the program.
Before I go on, a couple of things to note:
- There was a mistake in my description of Life last week; any time I made a reference to the number of “neighbors” a cell had, I was counting the liveness or deadness of the cell itself as counting toward the “neighbor” total. The program behaves the same way however you do the counting, but this means some of the numbers from my description last week aren’t the same as the ones this week.
- Because some of the images in this week’s post are kind of large, I posted all the images as the non-animated first frame, and you have to click the image to see the animated version. I assure you that scanning through here and clicking for the linked pictures this is probably more worth it than actually reading the text.
So, what’s this about quantum physics?
I’m still trying to figure this out, but this is what I’ve got so far: Quantum physics is a special very weird kind of way of looking at the universe where things aren’t ever one particular way, but are probably one of a bunch of different kinds of ways. If a particle is heading down a path and reaches some kind of fork where it could equally likely go either one way or the other, it possibly goes both ways at once, so we say it’s 50% at the end of one of the paths and 50% at the end of the other. It stays in this noncommittal state until some kind of interaction with the environment happens in a way that requires it to actually be in either one place or the other, at which point the particle randomly picks either one or the other and materializes 100% at the end of the paths as if it had been heading that way all along. As soon as this “wavefunction collapse” style interaction is over and the environment is looking the other way, the particle smears back out into possibilities again and starts again taking all the different paths it could at once, but now only those paths that start from the point at which its probabilities last collapsed. The splits in the paths it takes usually aren’t as simple as 50% one way, 50% the others– usually instead it goes in absolutely all directions at once, and its position is described by something called a “distribution function” that describes all the different things that particle could be doing at some given moment, and how likely each possibility is compared to the others. Because of something I don’t understand called the “Schrodinger equation”, the way these particles probabilistically spread out in every direction at once means they act like waves, which is where the “wave/particle duality” thing you hear about sometimes comes from– particles spread out as waves of probability until they encounter something that needs them to be a particle, at which point they switch to being particles, and after that they start spreading out as probability waves again. (We as humans don’t ever experience things that have this probably-there quantum behavior, like cats that are simultaneously alive or dead– the things that have quantum behavior are all very small, and things like cats or pennies or humans are very large, so by the time you start getting to interactions big enough that they can comprise our everyday experience all the little quantum things have been overwhelmingly spooked into acting like particles as far as we can tell.)
From a math person’s perspective, this whole thing about distribution functions that collapse into certainties upon measurement all just looks like a very contrived way of describing a system where you can’t make exact predictions about some of the things that happen and instead have to describe the probabilities. There’s a weird twist, though, because it’s more than that. When we talk about a particle being 50% in one place and 50% in another, we don’t just mean that there’s a 50% probability, if somebody barged in and collapsed the wavefunction, that the particle would turn out to have been there. The particle actually is there, in a 50% sort of way, and so all the different probably-there versions of the particle engage in something called “self-interference”, which means the different possible particles can interact with each other. If the particle goes 50% down one path and 50% down another, and then the two paths suddenly converge back again, the two 50% particles can actually smash into each other (destructively interfering with each other the same way waves do) and destroy each other at that point. All this weird behavior is kind of odd and interesting, and seems like it would be kind of fun to just play around and experiment with. Playing around with quantum mechanical objects, of course, requires either enormous and expensive test equipment that doesn’t do what you want anyway because of the Heisenberg Uncertainty Principle, or simulating everything with really really difficult math. The second of these sounds more attractive, and the fact the math is really hard probably isn’t such a problem; maybe one could make some kind of simulation program where the computer does all the math and you just mess around with stuff on the screen acting quantumy.
If you were going to do that, though, the obvious, particle-based stuff that quantum physicists spend most of their time working with doesn’t seem like the best place to start. Actual quantum physicists are mostly interested in hopelessly dry and practical things, like the behavior of electrons. There’s a good reason for that, but this sort of thing probably wouldn’t make for a very interesting or attention-capturing experience for someone just wanting to play around with something on a computer. I for one cannot say that electrons have much applicability or relevance to my daily life.
Given this, I was curious what else a Quantum Something simulation on a computer could be based around besides just particles. And I was thinking a good place to start would be cellular automata, like the Game of Life, because at least in the classical version they’re simple enough to be played with by clicking around at random but have enough hidden depth to make little machines out of; and also because they’re readily adaptable to acting like little nodes on a funny-shaped grid, which is incidentally the way that this “quantized geometry” thing that some guantum gravity people are moving toward lately looks from the perspective of a computer. A quantum Game of Life seemed like an interesting idea, so for my blog post last week I made a little animated GIF generator that ran the Game of Life, with the addition of “probable” cells which had a certain probability of either being there or not being there (with higher or lower probabilities represented by darker or lighter shades of gray) in hope of simulating or at least mimicking quantum behavior. As I said before, this didn’t really work.
Why not?
I’m not sure what I was expecting to see when I turned the thing on, but I think I kind of hoped that the patterns would act kind of like the maybe-there maybe-not particles in quantum physics– like, I perhaps expected that one way or another you would be able to make little partly-there patterns, like maybe a little 50% glider or something, and it would wiggle off in a 50% way until it collided with another glider, at which point depending on what hit what and how probable it all was maybe they’d destroy each other or merge into one 100%-there object or maybe even spin off several different overlaid collision patterns at the same time representing different probable results that the collision could have produced. In retrospect, it’s pretty obvious why it was completely implausible to expect behavior like this.
Patterns in “quantum Life” did in fact turn out to exhibit something like self-interaction. Unfortunately, they exhibited much too much of it. It isn’t just that patterns in Life interact with each other; every single cell in Life interacts with every single cell neighboring it, and one cell more or less worth of neighbors tends to make the difference between life or death in the next generation– the survival conditions in Life are extremely narrow. These properties– every cell interacts with every other, and you only get what you want under narrow conditions– is in fact what makes classical Life patterns capable of such complexity and thus interesting to study in the first place. In the quantum version of Life, though, these properties mean that if you introduce just one “gray” (probable rather than certain) pixel into the quantum Life board, then in the next generation every cell that pixel was touching will also be some shade of gray. And when you start getting a few grayish pixels next to each other, everything just kind of falls apart– fill an area in this conception of quantum Life with gray, and on every turn you’re basically trying every single combination of living and dead cells possible in that space, with some combinations maybe being more likely than others. Since only a narrow range of configurations allows life to survive in Life, this meant that each gray pixel tends to become less and less likely to survive with each frame, and gray areas very quickly fade to apparent white:
 |
 |
Interestingly, though, they don’t fade directly to white– they first try to stabilize at a specific gray value around a probability of 35%, with the 35% gray areas spreading to swallow up all the black pixels. If this 35% gray color manages to spread to cover the entire board, with each pixel being about as likely as any other, it just stays that way forever. If any areas that are at (or have stabilized near) 0% white exist on the board at all, however, the white eats away at any gray areas (or at least those that aren’t actively eating up new 100% black pixels) until nothing appears to be left. In practice this looks to me kind of like a zombie invasion spreading to eat all the Life and then dying out for lack of food:

Which is kind of amusing, but makes it really hard to do anything with the gray cells. In normal Life, where things are always either dead or alive instead of just probabilistic, you can build little Life machines by taking advantage of structure in the regular ways that the cells interacted with each other. In the quantum Life game, though, any structure is immediately destroyed as soon as it comes into contact with a gray pixel. Pattern-building in Life is based around individual pixels interacting with each other; but in quantum Life individual pixels lose their identity, and instead just smear out into rapidly disappearing gray blobs. This is about as far as I got by the end of my last blog post about this.
This week, my thought was: Before I give up on this completely, maybe I can at least get the blobs to do something interesting. If the tendency for everything to turn into blobs means I can’t build structures out of individual pixels, maybe I can at least build structures out of the blobs. Before I could do that, though, I first had to do something about the whole fading-to-white problem, since few if any of my patterns survived long enough to analyze them in an interesting way. I came up with two ways of getting around this problem. The first was just kind of silly, but I was curious what it would do so I tried it. The second thing I tried actually worked quite well.
As far as the first thing I tried goes, here’s the thing: Everything fades to white in these animated GIFs, but that’s partly just a result of the way they’re rendered. After the gray fades away, there’s still stuff going on in the apparently blank areas; it’s just that anything less than 0.0015% probability winds up being rounded down to 0% (white) when colors are picked, so you can’t see them in the GIFs. Likewise, even when everything appears to have stabilized at 35% gray, some areas will be closer to that stable gray point than others. I kinda wanted to see what this all looks like, so I changed the program so that it “normalized” each frame before it drew it– that is, instead of black being 100% and white being 0%, it redefined black and white as just the highest and lowest probability values visible on that frame. This lets us watch exactly what’s going on while various things are fading out:
 |


If you’re wondering what happens at the end of those animations there, that’s what happens when the probabilities at each pixel get so low that Perl can no longer accurately represent them. Perl only uses 64 bits to store each floating point number; this is normally way more than you need, but when you start trying to fit really, really low numbers into that space, like around 2-1022, you start losing precision and eventually lose the ability to tell the difference between any given number and zero entirely. With the kind of math the quantum Life program does, you get into this area pretty quickly, and with the normalization turned on the rounding errors that result become very clearly visible. Oddly, though, the rounding errors turn out to look a lot more interesting than the quantum Life program does when it’s operating normally. I may try to experiment with that more later, to see if I can replicate that behavior on purpose (hopefully this time by just rounding things instead of actually breaking the Perl interpreter).
After moving on from the normalization thing, I had a bit more luck with the next thing I tried. That was this: okay, so Life tends to turn into disappearing gray blobs when you add probability to it. Life isn’t the only standard cellular automata, though. Why not just try another one?
The set of rules Conway’s Life uses are really a bit arbitrary, and there’s a lot of variations on those rules out there. Life, because it’s the best well known and because it behaves in a way that exhibits a relatively nice balance, is the variation you generally hear about, but there’s nothing particularly special about it; to someone exploring the alternate rules, Conway’s Life becomes just the rule with serial number 23/3 (because life survives if it has two or three neighbors, and spawns if it has exactly three neighbors). Beyond this there are in fact 262,144 different 2D cellular automata rules of the same type (that is, where the rules are unchanged besides the survive/spawn numbers), and they all act very drastically different. Some of them are sane models of computation, like Conway’s Life, where you can build things out of patterns of pixels. Some of them inevitably descend into seething masses of chaos. Some of them just result in the screen endlessly blinking, or everything you draw exploding, or even stranger things happening. If you want to be really surprised, try loading up this Flash version of Life, entering rule 1234/3 (which you’ll note is not all that different from the Conway’s Life rule), drawing a little pool of pixels, and hitting “run”.
And 262,144 is of course just the number of variations you get by varying the survive/spawn numbers; you can get even more elaborate behaviors by introducing more complicated rules, for example by introducing more states besides just “alive” and “dead” or by allowing survival to be based on pixels further away than immediate neighbors. There’s one famous CA variant called Wireworld that is a lot like Life except for having four colors instead of two, and which can actually be used to present fairly realistic-looking simulations of electrical circuits.
(If you’re bored and want a quick little tour of a more complicated type of ruleset, go here, download the program or launch the java app, and do this: Choose “weighted life” in the first menu; choose “Conway–” from the second menu; hit “start”, and let the game run until the number of dots remaining on the screen is fairly small, then hit “stop”; choose “Border” from the second menu; hit “start”, and let the game run until the screen looks like television static; hit “stop” and choose “Bricks” from the second menu; hit “start” and let the game run until you get bored of what you’re seeing; hit “stop” and choose “Career” from the second menu; then hit “start”… each of these different options in the second menu is a relatively simple Life-like rule, with the only twist being that in these rules the direction your neighbors are located in makes a difference when counting. Even slight differences in what you do after you’ve counted these neighbors results in drastically different behavior.)
So, with all these cellular automata variations out there, is there an existing ruleset that fixes my blob problem? It turns out, yes. There’s a rule called “Day & Night”, a vanilla Life-alike with the rule 34678/3678 (you can try that in either the Java or Flash Life implementations above).
 |
| This is what happens when you try to feed a Conway’s Life glider into the Day & Night ruleset. |
This rule has a lot of similarities to Life from a pattern-designer’s perspective; it has simple gliders and spaceships and oscillators and such, although they look nothing like the ones in Life. However, Day & Night also has one very odd and interesting feature, which is that under the Day & Night rule, white patterns on a black background and black patterns on a white background behave exactly the same. You can randomly invert the entire board, and it will not change the way the patterns act one bit. More interestingly, you can actually have entirely separate black and white areas to the board, with little Life patterns swimming around inside:

This pattern seemed almost tailor-made to my problem: all my quantum Life patterns kept eventually stabilizing into invisible, boring white, but in Day & Night both white and black are stable. So what happens when I try to run a quantum Day & Night?
Well, this:


Okay, so this is a bit more interesting than Life was. Instead of the probabilistic parts just fading out of existence, the dark regions stabilize to black, the light regions stabilize to white, and the stuff in between stabilizes to some kind of midlevel gray. Things don’t stop there, but what they do next is kind of interesting to watch: The gray areas (although they never seem to go away after any amount of time) shrink until they become just a thin membrane between day and night, and the borders twist and curve according to some internal logic I haven’t quite figured out yet– I think the borders seek whatever position minimizes surface area, so to speak. (It’s kind of interesting to see the little bubble in the second image above slowly seeking air…)
Like in quantum Life, any single gray pixels introduced into an image spreads like a cancer over the entire board, but instead of this being an effectively destructive process, the “zombie” regions form into interesting patterns along the outlines of the black and white regions they follow, and the zombified regions continue evolving, just not according to exactly the same set of rules. The following board has one gray pixel buried in the upper left corner, and when Day & Night runs on it:
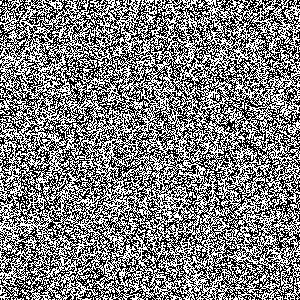
Something interesting you might notice about that one is that since the zombification process mostly acts on the borders of the day and night regions rather while leaving the interiors mostly solid, you can have little bitty Day & Night patterns embedded inside of the big gray blobs that just float there indefinitely doing their own thing (they’re still visible in frame 1000). In fact, it’s possible for there to be blocks which are zombie-ized on one side but continue to follow normal Day & Night rules on the other. Look at this one carefully:

Now that just looks cool. That last animation is seriously my favorite thing out of anything that’s come out of this silly little project so far. (Incidentally, if you want to see that a little more clearly, it may be worth it to try the YTMND version. Something not quite obvious in the images the way I’m posting them here is that since my implementation of Life wraps around the board at the edges, all of these images tile fantastically well.)
The fact that Day & Night supports stable areas of both colors means that I can do more elaborate things when setting up quantum Day & Night patterns. For example, something I wanted to do with quantum Life, but couldn’t really because everything always just disappeared, was set up patterns made from photos. Yes, both of these are starting patterns for animated GIFs:


Whee! Just for reference, here’s what if I round those last two off to solid black and white, so the quantum-ness goes away:


Finally, a couple more odd-looking results I got more or less by accident while playing around:
The one on the right does what it does because of a bug.
So, at this point I’m feeling a lot better about the possibility of actually doing something interesting with this probabilistic/quantum Life idea, now that I’ve seen it’s possible to do anything. The behavior of the white vs black blobs in this one still way favors entropy over structure– once the borders between white and black have been staked out they seem to do some kind of funny seeking-minimum-surface-area thing, and once they’ve done that (at least insofar as experimenting with firing spaceships at them seems to indicate) it doesn’t seem to be possible to move them back. You can of course still have normal Day & Night patterns happening inside the blob, but you could do that anyway; the quantum-ness doesn’t really add anything. Still, the Day & Night stuff at least works well enough it hints you could modify the rules so that the blobs were induced to interact with each other in some more interesting way. After all, I’ve still not even toyed with most of the different kinds of rule variations for cellular automata, and there’s even a couple of interesting options that may be worth exploring that only exist because of the probability thing. Meanwhile, there’s still a lot I could do here to work in math that’s actively taken from quantum physics, rather than just mimicking quantum-ness crudely. As things are, I’m not sure my conception of self-interaction is quite like that of “real” quantum physics, and I’m wondering if there’s some way I could work in a more explicit notion of quantum superposition (the way I do things now, basically each pixel is its own basis state). To be honest, I’m not really sure that deserves the title “quantum Life” rather than just “probabilistic life”.
I’m not sure to what degree I’m going to try to explore all that, though. In the meantime, I’m more curious about going back and starting to explore the original idea that had me thinking about quantum cellular automata in the first place: specifically, the idea of making a cellular automata that runs on, instead of a grid of pixels, the nodes of some kind of graph. And the reason for doing this would be that the graph would be not just a graph, but actually an instance of some kind of quantized geometry, like the spin networks in loop quantum gravity. Which would that mean… well, I don’t have any idea what it would mean. That’s why I want to do it and find out.
If I’m going to do that, though, I first want to stop and deal with something else, which is the way I’ve been making these little animations. Everything above was generated by a little perl module; I load the module up with starting states, and it spits out animated GIFs. This has more or less worked fine so far. There isn’t really any better way of posting Life animations than a GIF, since every pixel is crucial and so this stuff doesn’t compress very well; the chief downside to making this way is that by I generally have to craft the patterns by sticking them into a program and running it to see what comes out rather than doing anything interactive, but that doesn’t matter so much since the program with the quantum behavior turned on runs much too slowly to be interactive anyway (although that may only be because I wrote it inefficiently– I haven’t even looked into optimizing it).
If I go further with this series, though, the next batch of stuff I do is going to be all weird diagrams of jumbled lines, like those old photos of spiderwebs spun by spiders on drugs. This kind of stuff compresses very badly as GIFs, compresses well as other things, and will benefit from some level of interactivity. I’m basically only telling you this so that I can link the last thing I discovered this weekend and two more pointless little animations:
OMG HAX
So it turns out that at some point while I wasn’t paying attention, these people made a free actionscript compiler called MTASC, and these other people made a free swf linker kind of thing named swfmill. You can use these to make Macromedia Flash movies without actually having to own or use Macromedia Flash. Or you can just say shove both of these, and use HAXE, an odd but elegant little EMCAscript derivative with strong type inference and other pleasant features that take away the dirty feeling that writing Javascript normally leaves you with. Haxe can be “compiled” either to vanilla Javascript, or directly into SWF files. The reason all of this matters is that one can use Haxe or MTASC to make Flash movies without having to draw a damn thing. Both of the following movies are totally generative; thanks to Haxe, I was able to just write a little half-page program that draws some lines and boxes and things, and the program runs in the Flash interpreter:

This is not particularly complicated or interesting stuff– this barely qualifies as anything better than “hello world”– but it works, the resulting flash files are tiny (the freezeframe GIF of the colored boxes animation above is actually larger than the animation itself), and the Haxe language seems expressive enough to scale to much more elaborate Flash programs.
I’ll see what I can do with all this in a future post.
By the way, the source code used to generate this week’s images is available here and here, same usage instructions as last time.